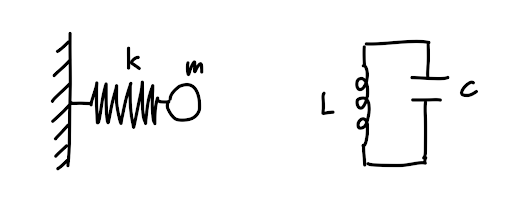“Not physics!” you sigh affer realising the Exsi article you just started reading is not about attaining a perfect state of mind, not about the beauty of water finding its way seawards, not about novel ways to perform chemistry, but about stone-cold physics. But maybe learning about flow isn’t too bad. I mean water is kind of interesting… Take, for example, the fact that if you wash a spoon, no matter what you do, the water always magically deflects exactly in your direction.

Maybe physics isn’t too bad, just this once.

You shall be disappointed once more when you realise that the flow in physics I am talking about has little to do with water, but rather everything with …everything.

The Noether Theorem

The beginning of the 20th century was marked by many revolutionary inventions and innovations in science, most famously perhaps, the inception of special and general relativity by Albert Einstein in 1905 and 1915. While Einstein’s contributions were remarkable in their postulates about the absolute value of the speed of light and the complexities of space and time, I will discuss another, less known, but arguably more important scientific revelation in this article. In the year 1915, the mathematician Emmy Noether proved the eponymous Noether theorem, believed by many physicists to be the most beautiful theorem in existence.

In short, Noether’s theorem states that every continuous symmetry is fundamentally connected with a conservation law.

You, dear reader, might now have a series of questions about the content and extent of this article, but don’t worry. I will keep myself as short as I want (which is not very short) First, I owe you an explanation of how this topic relates to the topic of flow:

Flow

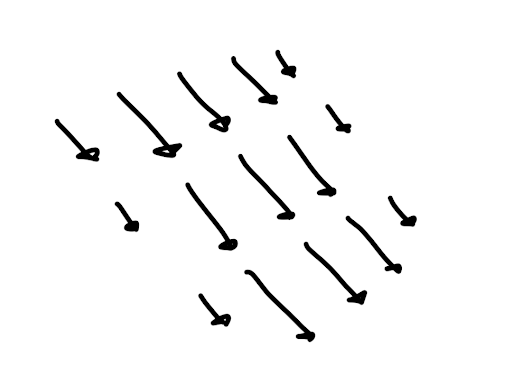
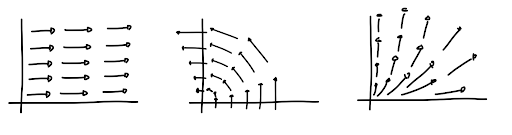
Imagine you want to simulate a river. What things would you have to consider, and how would you go about modeling these things with physics? A river definitely has some speed, and this speed is probably not the same at each point, which means we need an object to hold the speed of each “particle” of water according to its position. One way to construct such an object is a function:

We also might want to know in which direction the river flows at a certain point, so we modify our function to take a position and output a vector, which designates the speed and the direction of the flow at that point. If we display this function, we might see something like this:

This thing we just created might be cool and all, but it’s not a river! It doesn’t even move, it’s just a bunch of arrows! To implement a flowing river, let’s think about how we see that a river flows in the first place. If all the small “pieces of water” looked exactly the same, like a perfectly clean and steady stream of water, it would be impossible to distinguish this river from a still image (this will be relevant soon). To be able to see the flow, we need to introduce some sort of marker. This is the same technique used in wind channels, where one adds coloured smoke to visualise the flow of the air.

The question our model now needs to answer is a di0erent one: we want to know how a marker deforms and moves over time. If we put a marker at each coordinate point, we could e0ectively see how our initial coordinates are deformed by the flow over time.

Not only that, we can even put shapes onto the grid and see how they flow!

At this point, you perhaps think back to the beginning of the article, where I mentioned that this article was explicitly not about flows of water! Aggravated by this evidently wrong advertisement, you start skipping to the next article, when you are reminded of the historical tangent this article went o0 on about half a page ago. Yes, this article did write something about the Noether theorem, this apparently “very beautiful theorem (trust me)” which still means nothing to you.

To change this fact we first need to talk about symmetry:

Symmetry

Symmetry is something we all, especially the chemists among us, have a keen intuition about. Offen in everyday situations, symmetry shows itself in mirror images, which can recreate one half of an object from the other.

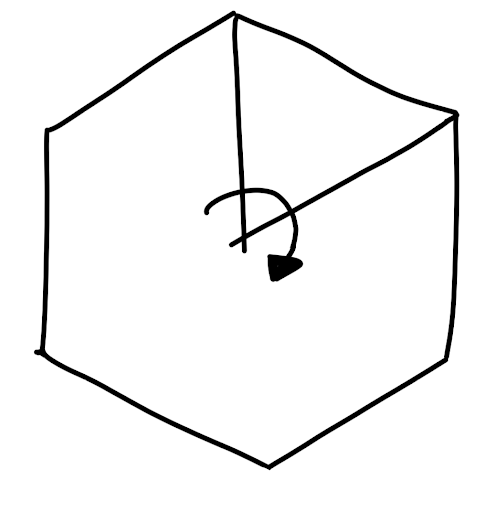
But mirror symmetry isn’t the only symmetry. For example a hexagon has sixfold rotational symmetry, meaning we can recreate the full hexagon from a sixth of itself by rotation.

Now more formally we call a thing X symmetric under the action A if doing A to X leaves X unchanged. We also say that X is A-invariant.

A hexagon, therefore, is symmetric under the 60 degree rotation. You can rotate a hexagon by 60 degrees and see no change. In other words: If you look away from a hexagon for even just a second, who knows how offen it has been rotated by increments of 60 degrees when you look back at it?! We will come back to this point in a second.

Now those symmetries are all discrete, meaning they take definite steps. The Noether theorem, however, only cares about continuous symmetries.

The idea of continuous symmetries is fundamentally the same as discrete symmetries, meaning that X is symmetric under A if A leaves X unchanged.

A typical example is the rotational symmetry of a circle. I can rotate the circle continuously without changing the circle at all (I promise it will make sense). The other symmetry we already saw was the translational symmetry of free space. If I move my empty universe around it’s still presumably the same empty universe (and would be indistinguishable from its original).

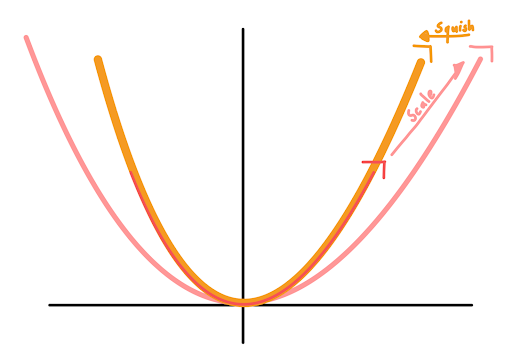
For a more abstract example, we can consider the scale-squish symmetry of the parabola (yes, that’s a name I just came up with). If I zoom out of a graph of a parabola, but adjust the y scaling in just the right way the parabola looks the same as before. Explicitly the transformation \(x\rightarrow x\cdot a\) and \(y\rightarrow y\cdot a^2\), which is the scaling \(x\rightarrow x\cdot a\), \(y\rightarrow y\cdot a\) and the squishing \(y\rightarrow y\cdot a\) gives us the same parabola again. Note that this symmetry was constructed from the observation that the parabola seems to grow less steep as we scale it up. To compensate for this fact we counteract this e0ect by squishing the parabola back into shape.

This is a continuous symmetry: we can vary as little or as much as we want, and the parabola doesn’t change. It is important to note something here. Just because the parabola is symmetric in respect to the scale-squish operation, or the circle is symmetric with respect to rotation, does not mean that everything, not even the parts of the object are symmetric. Consider a segment of the circle, this segment is obviously not invariant under rotation. Nor are segments of the parabola for that matter.

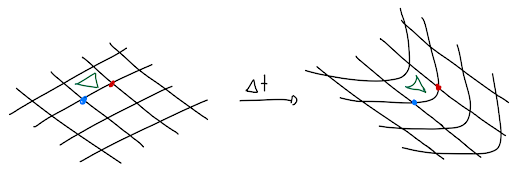
I have shown you some examples of continuous symmetries. But generally, what IS continuous symmetry? Well, I’m glad you asked. A shape X has the continuous symmetry of a flow A, if I can draw the shape onto the flow and no matter how long I wait/ let the flow flow, the shape remains unchanged.

For the flow I drew above (Figure 1.2), the lines along the flow are symmetric under it, as they do not change, no matter how long I wait. In general, If my shape follows the current, it is symmetric under that flow.

We can try to apply this flow formalism to the examples we already know.

As you can see, we can generate such a flow for any continuous symmetry. These flows are called Noether Currents, and they make up the first half of the Noether theorem.

Invariance

But why do we care about such symmetries? What does it mean, physically, for a system to be invariant under the flow A? Let’s first consider an example: Imagine a \(\ce {N2}\) molecule vibrating in space. Moving this molecule will not change anything about its physics. This system is translation invariant. In flow terms this means that if we apply the “everything flows from leff to right” flow (call this A), no matter how long we apply this flow, the molecule will remain unchanged (except its position, but because we have no other molecules to reference its position to, this position is arbitrary). We note, however, that no matter which way we move the system (or let it flow for that matter), there are some things we cannot do. We can, for example, never let the system flow in such a way as to excite a vibration. This is due to the fact that exciting a vibration evidently changes the system, meaning such an action cannot leave the system unchanged and therefore, the system cannot be A-invariant.

From this example we can extrapolate the meaning of A-invariance. Letting the system flow with A doesn’t change anything within the system (that’s the definition). But what this also implies is that any dynamics the system already has (if the system already behaves in a certain natural way, like the intrinsic vibration of \(\ce {N2}\)), we cannot reproduce this behaviour with our flow. If we could, we could make physically relevant changes on the system by letting it flow with A, which would contradict the premise that A leaves our system invariant.

In short, if our system is invariant under A, then anything really happening in our system is completely distinct from whatever A does to the system.

Conserved Quantities

To remind you of what we are trying to do, I will re-state the Noether theorem:

Every continuous symmetry has a conserved quantity.

We saw the continuous symmetries, and the way we model them with currents. Now where is the conserved quantity? The rigorous answer is the following: “The conserved quantity is given as the projection of the conjugate momentum onto the flow”. What do we mean by that? It means that momentum along the flow is conserved. As long as we go with the flow, we don’t change our momentum. Which makes sense, because if we did, then we would end up in a situation where our flow, which is supposed to leave our system invariant, causes a change in the system!

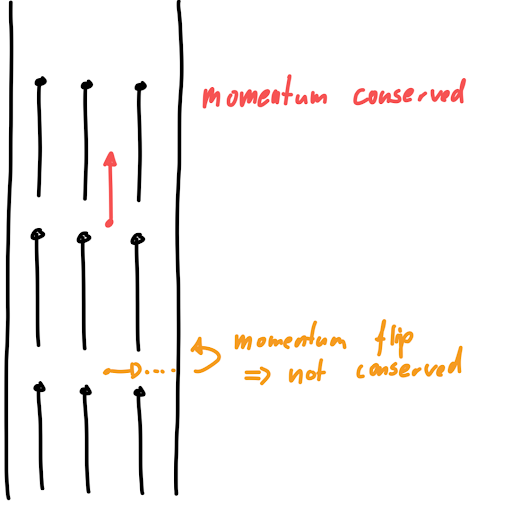
It is important to note that momentum which is not along the flow does not need to be conserved. – Why? Because while our flow keeps the full system invariant, it does not guarantee that parts of the system stay invariant (like the circle/circle segment example above). Explicitly, this means that by going to a di0erent part of the flow (by not following it) we can driff very far away from where we started originally.

Take, for example, a particle in a tube. Along the axis of the tube we have translation invariance (we assume the tube to be infinitely long). Using the Noether theorem we can create the displacement flow (flow through the pipe), which shows us that the momentum projected onto this flow is conserved. Now what happens if the particle hits a wall because it was moving at an angle to the flow? It suddenly flips its momentum when it is reflected. We see that momentum along this axis is not conserved!

Now we were talking about classical momentum, but there is one last concept from general mechanics I don’t want to keep from you: Conjugate momentum.

Momentum and Beyond

The idea behind conjugate momentum is the following: The position variable \(x\) in our equations of motion is in the end just a mathematical symbol with no meaning attached. If we free ourselves from the idea that \(x\) needs to be a position we can find something marvelous: Any two variables that have a value and can change in time that are represented in the physical system can be related to each other as “position” and “momentum”. As an example, let’s compare the energy of the harmonic oscillator:

with the energy in an LC circuit

Note that \(v=x'\) and \(I = Q'\).

Looking at the formula for the energy, we realise that even though the physics is fundamentally di0erent, the maths is not. As a matter of fact, we can simply assign \(k=\frac {1}{C}\) and \(L=m\) and obtain the exact same equations.

Let’s interpret this mathematical “coincidence” from a physical standpoint: We know that the harmonic oscillator has momentum, so the circuit also needs some kind of momentum. The momentum in the oscillator is \(m\cdot v\) thus by analogy the “momentum” of the LC circuit needs to be \(L\cdot I\). This coincidentally gives us a very relevant quantity from electronics, the voltage \(V\)! So we learn that in this system \(V\) is the conjugate momentum to \(Q\), and we can apply all of our fancy maths to not only this system, but also to basically any other system that contains variables whose change is governed by a Hamiltonian!

To elaborate a bit on the use of conjugate momentum, if we imagine time as a fourth dimension, and we note that the physics in our system is time independent (as in the forces don’t change over time). We find that our system is time translation invariant. This means that doing physics now should be the same as doing physics tomorrow. We can even find the conjugate momentum to this time translation, which should be conserved. If we do the maths (which is a bit more elaborate than what I am describing) we find that the conserved quantity from time translation invariance is energy. In short, we can figure out that energy within our system is conserved from the fact that physics is the same now and tomorrow!

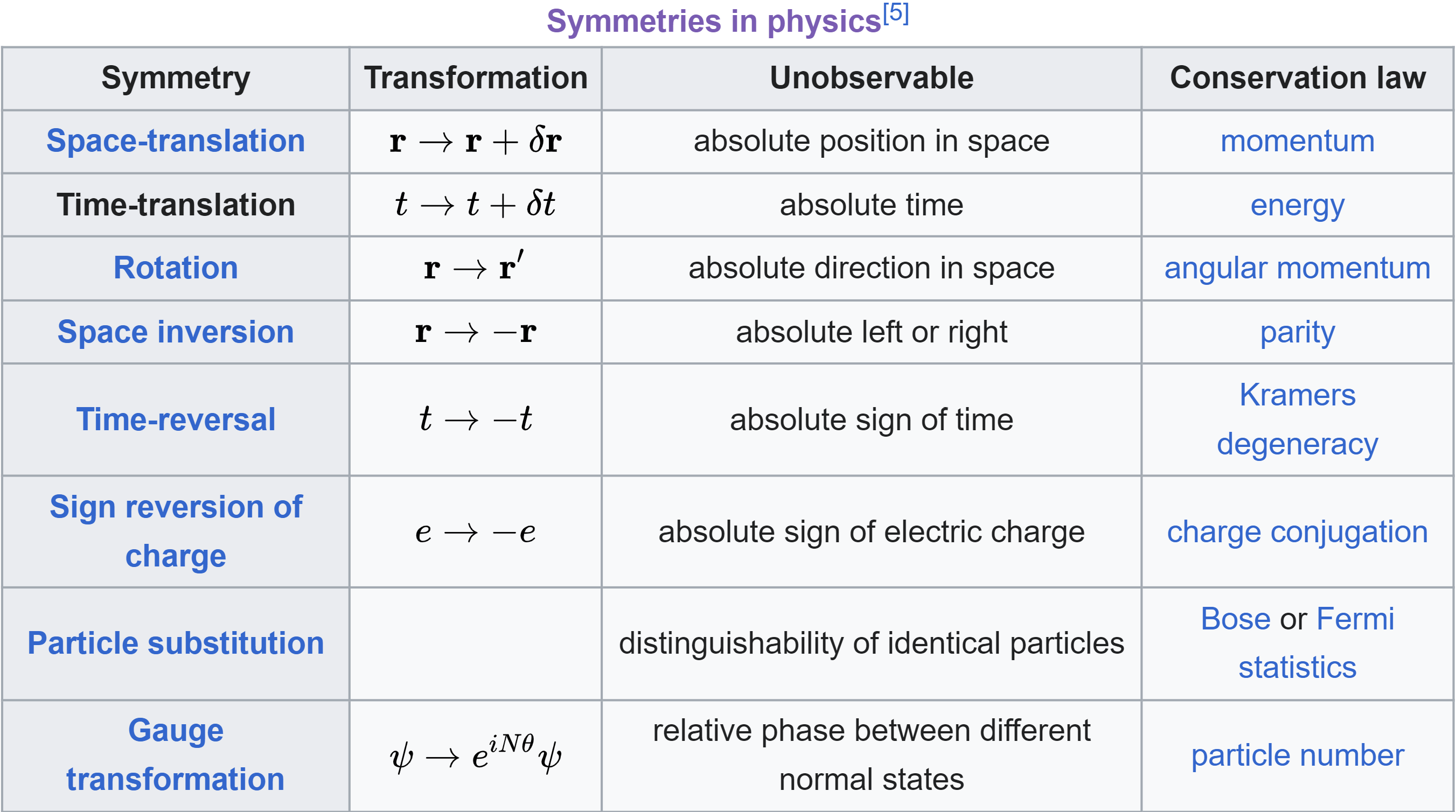
There are a bunch more invariants we can derive from symmetries of our universe. Figure 1.8 is a list from Wikipedia.

Conclusion

The Noether theorem states that for every continuous symmetry there exists a conservation law. We can find this conservation law by expressing the continuous symmetry as a flow which leaves our system unchanged. Going along with this flow we see that momentum is unchanged, while cutting across the flow will not guarantee the same. Momentum can be interpreted more generally than we know it. The most general form of momentum is the so-called generalised or conjugate momentum to a quantity. It expresses how the quantity it is conjugated to should evolve in time. Combining these two concepts, we can find conserved quantities from symmetries in any physical system, giving us a fundamental insight into how our universe works! And as a small bonus we learn a little lesson in life: When in doubt about what to do, the universe will always tell you: Just go with the flow!

Bibliography