### Polarisationschaos:
Quellen der Verwirrung, die ihr im Kopf behalten solltet:
- Orientation der $z-Achse$
- Negatives Vorzeichen der Zeit $\xi = \cos(kx-\omega t)$
- Orts/ Zeitbild
Die Daumenregel:
1) Zeige mit Daumen in Richtung Propagation
2) An einem fixen Ort, betrachte die Bewegung des Polarisationsvektors
3) Wenn die Finger in Richtung des Polarisationsvektors drehen -> Drehung der jeweiligen Hand
Polarisation Overview (werde ich noch mit Prof. Abklären):
| Eigenschaft | | |
| --------------------------------- | ------------------------- | -------------------------- |
| Zirkularität | Rechts (im Uhrzeigersinn) | Links (Gegenuhrzeigersinn) |
| Phase auf y | $\frac{+\pi}{2}$ | $\frac{-\pi}{2}$ |
| Händigkeit der Schraube bei $t=0$ | Links | Rechts |
| Drehrichtung fürs Einschrauben | Links | Rechts |
### Wellentypen:
Wir charakterisieren Wellenfronten mithilfe der Flächen gleicher Phase. Dh. diesen Punkten wo das Argument von der Wellenfunktion gleich ist.
Für $\xi(\vec x,t)= f(\vec k \cdot \vec x-\omega t)$ bedeutet dies diese Punkte wo $\vec k \cdot \vec x - \omega t = const$
#### Kugelwellen:
#### Ebene wellen:
Phase in jeder Ebene senkrecht zur Ausbreitungsrichtung unter sich selbst identisch
### Reflektion/Transmission
Wenn eine Welle das Medium wechselt, müssen wegen der Stetigkeit einige Bedingungen erfüllt werden.
- Frequenz bleibt gleich
- Wenn die Frequenz sich ändern würde, so würde bei der Grenzfläche die Welle eine relative Phase aufnehmen (dh. Die Welle hätte einen Sprung bzw wäre nicht mehr synchronisiert)
- Die Geschwindigkeit und die Wellenzahl bleiben im Allgemeinen nicht gleich.
### Intensität/Poynting vector
**Energiedichte** $\dd WV$
Die Energiedichte entspricht im mechanischen Fall der kinetischen plus potentiellen Energie pro Volumen. Dies ist jedoch nicht universell.
Wir können eine Welle als ein “hin-und-herschaufeln” von Energie betrachten. Die Energiedichte entspricht dann der Energie in beiden “Reservoirs” zusammen pro Volumeneinheit.
Es ist wichtig zu bemerken, dass $\dd{W}{V}$ nicht konstant ist, wie man vielleicht durch das Oszilatorbild denken würde. Der Grund dafür ist die Kopplung zwischen den Oszillatoren (genau der Grund warum wir überhaupt Wellen haben)
**Mittlere Energiedichte** $\langle \dd WV \rangle = \frac{1}{T}\int_{0}^{T}\dd{W}{V}dt$
Wir können jedoch die durchschnittliche Energiedichte betrachten. Diese ist insb dann relevant wenn die Frequenz sehr hoch ist (wie zB bei Licht (THz-PHz))
**Energieflussdichte** $\bf{S} = \dd{^2W}{A dt}\hat n$
Hinweis: Für Aufgaben mit der Energieflussdichte lohnt es sich oft zu vergleichen welcher Teil der Gesamtleistung beim Ziel ankommt. (Beispielsweise nimmt die Energieflussdichte von Kugelwellen mit dem Quadrat des Radius ab (da eine gewisse fläche einen immer Kleineren Teil der Gesamtfläche ausmacht))
**Intensität** $I=|S|$
Der Poynting vector ist oft overkill, durch einfache geometrische Überlegungen reicht auch oft der Betrag davon. Dies nennen wir die Intensität
## Diese Woche
### Stehende Welle
Betrachte 2 Wellen: $$\cos(kx - \omega t) + \cos(-kx -\omega t + \delta_R) = 2A\cos(kx)\cos(\omega t)$$ (mithilfe $\cos(a)\cos(b) = \frac{\cos(a+b)+\cos(a-b)}{2}$)
Bemerke, dass wir jetzt Zeit und Raum komponenten getrennt haben, welches qualitative verhalten erwarten wir?
#### Hartes vs Weiches Ende:
Wie wir bereits aus der normalen Reflektion gesehen haben, gibt es zwei qualitativ unterschiedliche Lösungen für die Reflektion:
1) Reflektion am harten Ende: Phasensprung, da nicht “die gesamte Amplidtude im neuen Medium Platz hat”
2) Reflektion am weichen Ende: Kein Phasensprung
Beispiele dafür sind:
1) Saiten
2) Blasinstrumente
(Merke, das sind die Grenzfälle der Letztwochigen Serie)
#### Energietransport
Wenn die Welle mal aufgebaut ist sehen wir (durch die Trennung der Orts/Zeitkomponenten), dass wir eigentlich für jeden Ort einen eigenen harmonischen Oszilator haben.
Wir sehen das Resultat auch, wenn wir die Energieverteilung explizit berechnen
### Huygensches’ Prinzip
Jeder Punkt emmitiert eine Kugelwelle, welche in der Überlagerung/Superposition zur beobachteten Welle führen.
Wellenfläche: $k\cdot r - \omega t = \delta$
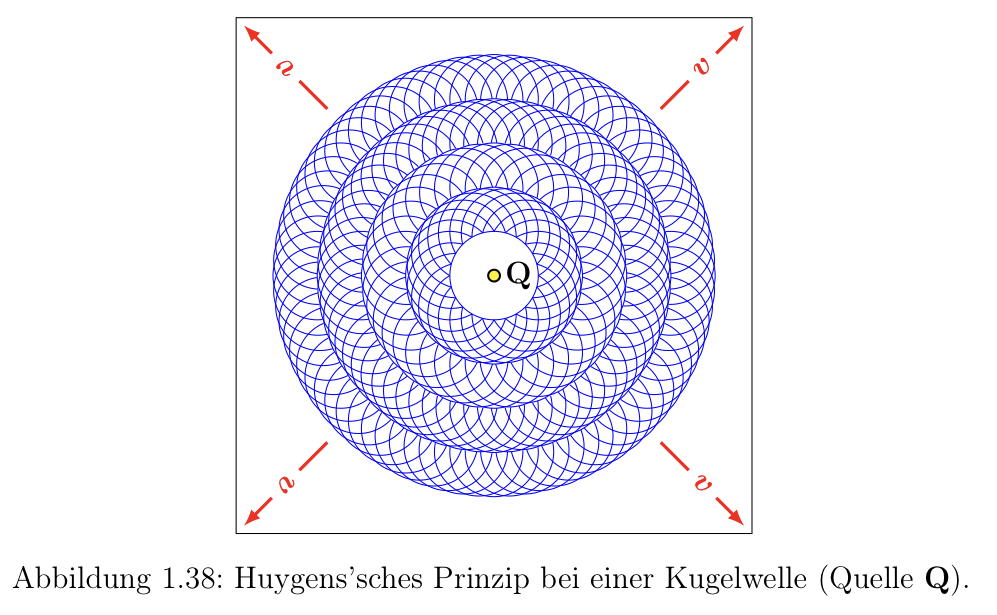#### Dopplereffekt
Der Dopplereffekt ist gegeben durch: (für sich annähernde Sender/Empfänger)
$$\nu_{empfänger} = \nu_{sender} \frac{1 + (\frac{v_{empfänger}}{c})}{1-\frac{v_{sender}}{c}}$$
Merkspruch 1: Annäherung -> gestauchte Wellen -> höhere Frequenz
Merkspruch 2: (Bruch oben unten): Für $v_{sender}=c$ gibt’s einen Schallknall (deckt das gesamte Frequenzband )
### Elektrostatik
Die Elektrostatik ist vollkommen in Analogie mit Newtonscher Gravitation:
$\vec F_{C}=\frac{1}{4\pi\varepsilon_{0}} \frac{Q_{1}Q_{2}}{r^{2}}\hat r$
Das EM Feld ist wie die Kraft, nur haben wir uns noch nicht auf eine Ladung geeinigt.
$\vec E = \Econst \frac{Q}{r^{2}}\hat r$
$\vec F = q \vec E$
Wir sehen, dass das Feld mit $\frac{1}{r^{2}}$ abnimmt, dies suggeriert, dass das Feld sich “auf die Oberfläche verteilt” (doppelter radius der Kugel -> viermal grössere Fläche)
Die Grösse die Konstant bleibt ist der Elektrische Fluss ($\Phi$) (nicht zu verwechseln mit dem Potential!!!)
$\Phi = \int \vec E dA$ (Alles Feld zusammen)
Zusätzlich bemerken wir, dass der Ursprung von diesem Fluss jeweils die Ladungen sind (Ohne Ladungen kein Fluss) (wir sehen das auch, wenn wir das Integral oben für eine Beispielsfläche durchführen)
$\Phi = \frac{q}{\varepsilon}$
Ein nützliches Tool für die Buchhaltung des Flusses sind die Feldlinien.
- Wir sagen wir verwenden pro Ladung eine bestimmte Anzahl Feldlinien.
- Jede Feldlinie Startet bei einer Positiven Ladung, und endet bei einer Negativen Ladung, oder im Unendlichen
Um das Feld an einem Punkt zu berechnen betrachte stelle ich die folgende Frage:
- Wie gross ist der Anteil der Feldlinien, die durch mein Flächenstück gehen
- $\vec E = \frac{\Phi}{A}\hat n$
Dies ist der Satz von Gauss
## MC
> Welche Aussagen sind korrekt?
- Das Huygen’sche Prinzip besagt, dass die Flächen gleicher Phase immer eine Kugel bilden
- Bei der Stehenden Welle wird die Energie immer zwischen den “Bergen” und “Tälern” hin und her transportiert
- Beugung und Brechung sind das selbe Phänomen
- Totalreflektion gibt es nur beim Übergang von einem dichten in ein weniger dichtes medium
> Auf einem Zug steht ein Saxophonspieler, er spielt einen ein C. Welche Aussagen sind korrekt
- Beim Vorbeifahren erklingt der ton zuerst tief, dann hoch
- Beim Vorbeifahren erklingt der ton zuerst hoch, dann tief
- Ob der Zug an mir vorbeifährt, oder ob ich am Zug vorbeifahre spielt keine Rolle
- Wenn der Zug im perfekten Kreis um mich fahren würde, gäbe es keinen Doppereffekt (Bonus)
> Bei einer Beugung am Spalt ist die Reihenfolge der Farben, von innen nach aussen:
- Weiss, Blau, Gelb, Rot
- Rot, Gelb, Blau, Weiss
- Blau, Gelb, Rot
- Rot, Gelb, Blau
> Welche Aussagen sind Korrekt:
**a)** Im mittelpunkt der Erde herscht keine Gravitation, aus dem Selben Grund, warum im Mittelpunkt einer Hohlkugel kein Feld exisitert
**b)** Das Coulomb Gesetz besagt, dass das Elektrische Feld nur von der Anzahl eingeschlossener Ladungen abhängt
**c)** Das Colomb Gesetzt besagt, dass das Elektrische Feld mit dem eingeschlossenen Volumen abnimmt.
**d)** Alle obigen Aussagen sind Falsch
### Bonus
#### Doppelspalt mit Huygens
