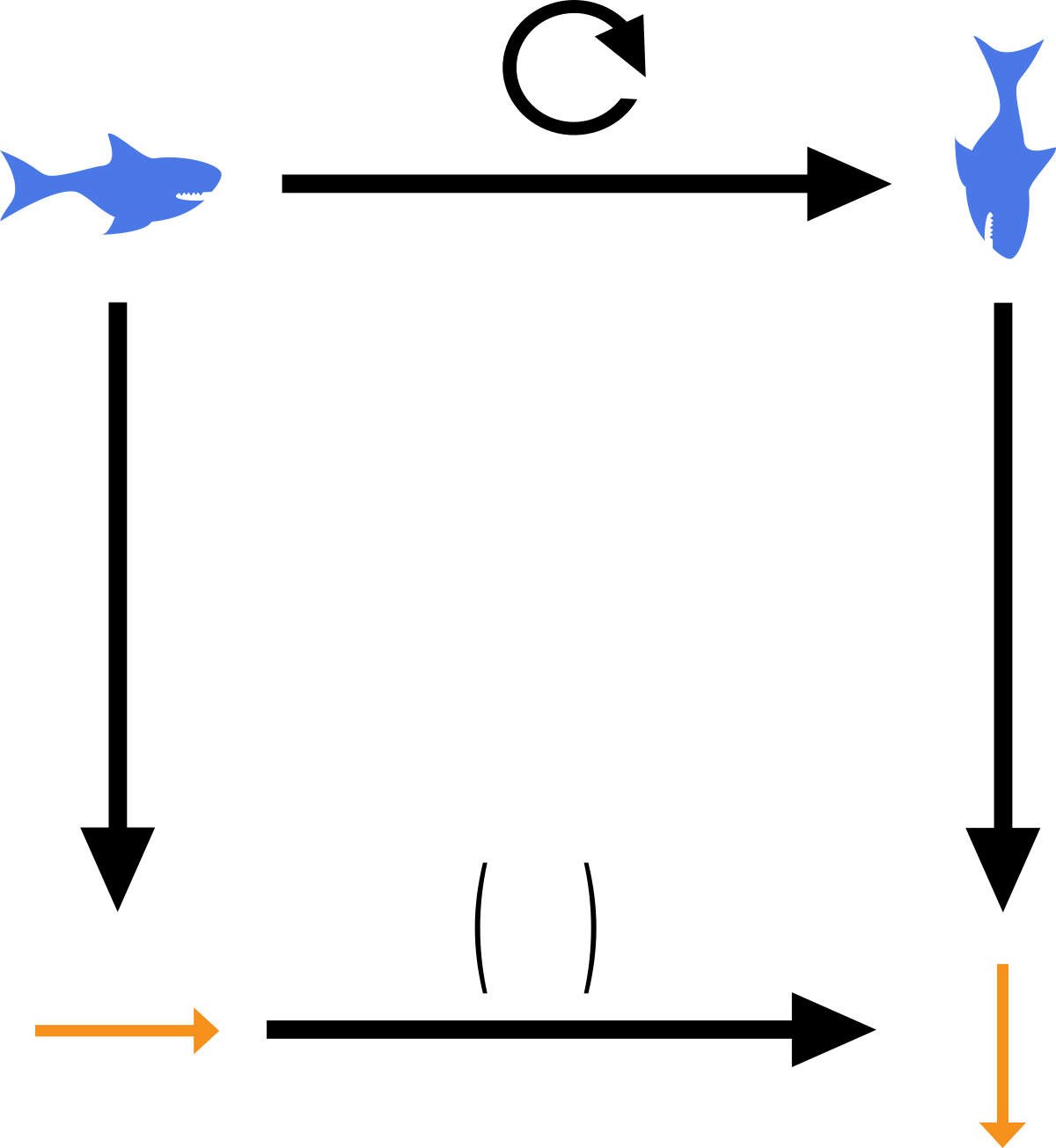
Imagine if you will, being a shark, minding your own business. Just swimming around the ocean floor. Due to your bilateral symmetry you can freely decide¹ to go leff or right. As long as the ocean floor is even we could call both options “degenerate”. Now what would you feel like if you were to, for the sake of argument, be rotated around an axis inclined at 45\(\relax \NoFonts \sp {\degree }\EndNoFonts \) to your spine (see Figure 1.1).

As the rotation axis did not preserve your symmetries, you would be rightfully confused!² You wouldn’t be half as confused if you had just been mirrored through the plane bisecting you, would you? The essential di0erence between those two scenarios lies in a simple word; symmetry!

But what does symmetry actually mean³ ?

Symmetry means exactly what it means

What happened here is a very obvious physical thing, but mathematically it is actually very interesting.⁴ We as humans are accustomed to the phenomenon that “doing the symmetry” on a symmetric object leaves it the same (Mirroring something along its mirror plane does nothing). And that doing something that “is not the symmetry,” changes it (Mirroring a non mirror symmetric object has to change it). Mathematically this connection is less obvious. How does a property of an object (symmetry of the shark) combine with an action on the object (getting rotated) to yield an object (rotated shark). And how does the result change depending on whether the actions and the objects symmetry match?

This is where group theory comes into play. Mathematically a group is a set with a binary operation that fulfills the group axioms Associativity existence of unique identity and existence of unique inverse.

Isn’t it annoying when people explaining something put complicated definitions in the text not to be understood but just to accentuate how “di0icult” the topic is that they try to explain?

Simply put, a group is a collection of things you can combine in pairs to get things of the same type again. A typical example for a group is the rotation group ⁵ you can take any rotation and then add (do) a second rotation, to yield a third combined rotation!

A symmetry then is the property of an object to not change upon application of the corresponding group operation. You might be wondering why I would want to separate symmetries as properties of objects from symmetries as operations on those objects. And wondering this, you are of course correct. Because mathematically we never even talked about the object in the first place. In reality we always take the approach:

1.

Take object, look at what operations leave it unchanged

2.

Throw away the object

3.

Only consider the symmetries of the object

So in e0ect by using the symmetries we are intentionally forgetting the details of the object. If you are a chemist, you have done this a billion times before, when reducing a molecule to its point group. From a point group you cannot go back to the molecule (because in the process you have thrown too many details away).

If we want to go back and explain the confusion of the shark we need only find its point group (\(C_s\)). Checking if \(C_s\) contains a \(C_{2d}\) axis will tell us if the shark ought to have been surprised. And oh wonder, if we check the character table of \(C_s\) we see no \(C_{2d}\) axis, which proves the point, the shark has every right to be confused (isn’t maths useful :D)

So why did I separate the symmetry operations from the symmetries of the object? Well there is a simple answer:

Sharks are not just a collection of symmetries!

To describe a shark fully we need way more information. More information in mathematics means more dimensions!

Parallel Orthogonal dimensions

What do I mean when I say more dimensions? Normally we think of dimensions as something physical, like the three dimensions of space, the two dimensions of a sheet of paper or the one dimension of a line. This mindset is limiting, because while we might be able to stretch our imagination to include time as a fourth dimension, trying to get geometric interpretations of 4D hypercubes will give you nothing but a headache. If we take a step back from the physical interpretations of dimensions and take a look at what they actually mean we realize something pretty neat. To illustrate let me ask you a few easy questions about dimensions you understand intuitively:

• How many things do you need to tell me about a block in a city for me to find it?
• If you know on which street I live, how much more information do you need to find my house?

The answers to those questions should be two and one respectively, the dimensions of the spaces the objects we were describing live in.⁶ If we continue that trend, the simplest thing we can say about a four dimensional space is that any point within it can be described with four coordinates!

Inversely this also means that if we have a thing that can be described using \(N\) numbers we can just pretend that this thing lives in an \(N\) dimensional space.

A pretty stupid example for this are IKEA chairs.⁷ Many chairs there you can buy with both di0erent wood and with di0erent pollsters. If I need to tell my friend which chair to buy I can tell them three things:

• Which chair model to buy
• what wood to choose
• and which pollster.

In essence IKEA chairs live in a three dimensional space. Note that those three ‘configuration-dimensions’ have nothing to do with the three spatial dimensions in which a chair lives, they are dimensions not of real space, but of configuration space. To accentuate this point, if I’m telling my friend where to put the chair affer buying it I need to tell them the coordinate (lets say at the back and right). The final resulting chair is now a five dimensional object (or a 5D-vector see Figure 1.2).

Going back to our shark we realize that to describe a shark we need many, maybe an infinite amount of dimensions. We immediately realize this is terribly inconvenient for any operation we want to perform on the shark. But luckily the mathematical branch of representation theory has our back.

Symmetry means shu0ling matrices

We saw previously that we can describe symmetries on objects by using group theory. And we saw that we can describe objects by using \(N\)-dimensional vectors. We might now ask how the symmetry of the object relates to the symmetry of the vector view of said object. There has to be a relation, because I can always create a ‘rotated vector’ by first doing the symmetry on the object and then transforming the object to a vector. Mathematicians express this possibility using a so called commutative diagram (see Figure 1.3):

We can see that we can follow both the upper and the lower part of the square to end at the same place. When we are asking about what the symmetry is on a vector we are in essence asking about the bottom edge of the square.

But before we find the exact identity of the symmetry we might want to find out what type of ‘thing’ this vector-symmetry will be. We know that the vector-symmetry will be a thing that maps a vector onto a vector. There is one object we know from linear algebra that does this trick fairly easily, matrices!⁸

Once we have found out how a symmetry acts on both the objects and on the vectors, we can associate the group action with the corresponding matrix by going around the commutative diagram.

This same procedure can be done for every symmetry in a symmetry group. The resulting mapping between symmetries and matrices is called a representation. It is important to note here that a representation of a group is not unique, quite the opposite actually! You see the type of thing on the bottom edge of the square really depends on the type of vector we built in the first place.

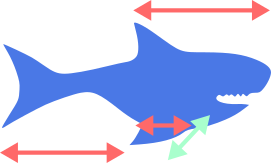
I’ll elaborate with a simple example. Let’s go back to the point where we defined a vector corresponding to our shark, we said there that we might need thousands of parameters to fully characterize a shark, and this is true. But what if we were lazy and really only cared about one or two properties of the shark. Let’s say we only care about the width and the length of the shark, our resulting vector have two dimensions, one for each of the two attributes.

We can still transform a shark into a vector. And we can still decide if we want to apply the symmetry to the shark, or the matrix to the vector. But now the matrix will be a 2 by 2 matrix. And of course the same holds for any number of attributes we might want to define of the shark.

To recap, a representation is a way to consistently transform symmetries to matrices. The size of the matrices depend on our encoding of the original object and representations are not unique.

Why would we care about this matrix and vector stu0 if we can just look at the object and the group actions? That is a fair concern and I know this representation theory stu0 can be extremely abstract, but the real reason why we keep up with these complications is that understanding how the general structure of representations work gives us a great insight into how we can simplify hard problems.

Symmetry means getting to terms with the complexity of the universe

We saw previously that there are many di0erent representations for a symmetry group. A logical question might be if there is a way to find which of these representations are useful.

To find which representations are useful we might want to find the smallest possible representation that still ’captures the symmetries’ of the object under study.

To find these smallest representations we need to understand what it means for a representation to be ’small’. The word mathematicians prefer to use here actually is irreducible. An irreducible representation or irrep for short has to be the smallest representation because it literally cannot be ’reduced’/ made smaller.

So what does it mean to be irreducible, or asked di0erently what does it mean to be reducible? Let’s quickly think about our poor shark again. We previously saw that the shark can be lazily described using the two dimensions of width and length. Let’s actually reformulate that a bit and call it core-to-fin-distance and length. Let’s try to explicitly construct a representation for this 2D shark. First the symmetries. We directly see that there are just two \(\sigma \) and the identity. One way to construct a representation here would be the following:

Both symmetries map the length onto the length (seen by the top leff one in the matrix). Where it becomes interesting is the bottom right. As you can see the mirror operation flips the core-to-fin-distance. Even more interestingly we see that it seems like there are two di0erent behaviors in both matrices, once the behavior of the top leff, and once the behavior of the bottom right. It almost looks like the length part of the shark works fundamentally di0erently to the leff/right part of the shark…
What if we just say the shark is only characterized by length? The resulting representation would be the following:

This is just a 1D representation! We also see this representation as the top leff of both of the matrices in the 2D example!
Let’s see if we can do the same thing by saying the shark is described by leff-span and right-span:

This is an other (di0erent) 1D representation! This one being the bottom right of both matrices in the 2D case!
Moreover it turns out that for \(C_s\) those are all the irreps there are!

Let that quickly sink in. What did we observe just now?
We took a look at di0erent properties a shark had and we found out that some properties transform di0erently to other properties. We then used that fact to find minimal combinations of properties that behave in this specific way. The first representation we found, the boring one was a property that did not change upon reflection. This irrep is offen just called the trivial representation. Other names for it are the completely symmetric representation the \(A_1\) representation or just \(A'\). It describes any property of the shark that is not a0ected by mirroring, in e0ect this means any property which lies on the bisection of the shark. The second irrep we found is offen called the antisymmetric representation or \(A''\). It describes properties that flip or exchange upon mirroring. Every property that contributes to the ’bilateral-ness’ of the shark will be represented here.

The way we would express the fact that this 2D description of the shark behaves in this way would be the following: \(A' \oplus A''.\) This means that the 2D shark is one part symmetric (the length) and one part antisymmetric (the fin-to-core-distance)

.

We can make our description of the shark more detailed and see how that changes which irreps make up our vector description of the shark. For this let’s consider a shark as the following 4D object (see Figure 1.4).

Here we describe the shark as a combination of the tail length, the snout length, the fin length and the fin-to-core-distance. By observing how the symmetries \(id\) and \(\sigma \) act on those measurements we see that three of them behave symmetrically (red), while one is flipped (green). The resulting representation is thus \(A' \oplus A'\oplus A'\oplus A'' = 3A' \oplus A''\). Translated this means that our 4D shark is three parts symmetric and one part antisymmetric.

This is pretty cool, because now we can decompose objects into their symmetry parts, we can say which parts of an object behave in a specific symmetric way.

Let me give you a more elaborate example, let’s consider \(\ce {Cr(CO)6}\). The point group here is \(O_h\). First consider the ligands as one block. To describe the complex we need to specify the distance between the ligands and the central atom, which amounts to six dimensions. Let’s try to decompose the full 6D representation into irreps I will spare you the math but you can look it up here if you are interested^[2] We could do the full reduction formula approach, or we can try to intuit what parts we would expect. First we can describe the complex using the metal-ligand distance. This is one number, that does not change upon application of symmetries. This means that metal-ligand distance is fully symmetric and transforms according to \(A_{1g}\). We now have 5 more dimensions leff. The second thing we could consider is the z-elongation, meaning how much the two ligands on the z axis are displaced from the average distance to the atom (think Jahn-Teller e0ect). To describe this elongation we will have two parts, the ’moving apart’ dimension and the ’moving together’ dimension. Thus the irrep needs to be two dimensional. Looking at the character table we see that we need to choose between \(E_{u}\) and \(E_{g}\). The major di0erence between the two is the action of \(\sigma _h\) on them. For \(E_{u}\) applying \(\sigma _h\) flips the property, while for \(E_{g}\) it remains the same. Both the moving apart and the moving together dimension stay the same upon application of \(\sigma _h\) which means this has to be \(E_{g}\). We are now leff with 3 more dimensions we need to explain. For this we will consider the equatorial ligands, there are four so we might be tempted to say we need a four dimensional representation, but it turns out you can fully describe the quadrilateral using three parameters.⁹ Affer some more consideration we will find that the resulting symmetry is \(T_{1u}\). The full representation is thus \(A_{1g} \oplus E_{g} \oplus T_{1u}\). Each of these representation describes

• The “total symmetry-ness”/the distance from the metal.
• The “axial deformation-ness”/the distance between the z-ligands and the center of mass o0set from the metal.
• The “equatorial deformation-ness”

. We can now find out how those ligands interact with our metal center. By applying the same representation theory on the d-orbitals of the metal we can see that the corresponding representation is \(E_{g}\oplus T_{2g}\). One of the irreps (\(E_g\)) matches, which means that hybridization is possible, which will stabilize the orbitals. The other does not match (\(T_{2g}\) and \(T_{1u}\)), meaning the \(T_{2g}\) part of the d-orbitals will not interact and remain non-bonding. This behavior explains exactly the splitting of the ligand field in the octahedral configuration!

The fact that symmetry tells us something about the energetic structure of a molecule is no coincidence. It is the direct consequence from one of the most central theorems in representation theory: Schurs lemma.^[6] In simplified terms it states that any function on a symmetric object, which preserves that symmetry (In physics the hamiltonian is a good example) will have solutions with the same “shape” as the irreps of the object. This means that if I find that my molecules symmetry is made up from one 1d one 2d and one 3d irrep any solution to a equally symmetric hamiltonian will at most have three solutions with degeneracy 1,2 and 3. This is why we can label degenerate orbitals with the symmetry symbols, they are directly coupled!

To summarize: We figured out how irreps are “fundamental building blocks” of symmetric objects. We have also seen some examples on how to interpret the irreps. Finally using Schurs lemma we managed to convince ourselves why symmetries can reduce the di0iculty of mathematical problems by restricting the solutions to the symmetries.

Symmetry means seeing beauty in nature

We are surrounded by a multitude of symmetries, some of them are evident like mirror and rotation symmetries. Others are more obscure like time translation symmetry. To end this dive into symmetry and representation theory I would like to show you my favorite applications of symmetry:

The Noether Theorem

For the people that haven’t read my article ’Go with the Flow’ in Exsi “Fluss”^[4] I will give a brief summary ¹⁰ . The fundamental statement of the Noether Theorem is that any conserved quantity belongs to a continuous symmetry.

It allows us to go from the observation that space is translation symmetric to the realization that momentum must be conserved!

Equipped with our new tools of representation theory we can now extend this understanding. In the Noether Theorem the symmetries need to be explicitly continuous, but using representation theory we can now also tackle discrete symmetries.

A adapted Noether Theorem might be formulated as such:

Any irreducible representation for the symmetry group of a Hamiltonian (read any irrep for the energy landscape) can be mapped onto a conserved subspace.

Essentially this means that if my energy relations are in a specific symmetry group (for example \(CH_4\) will have a \(T_d\) Hamiltonian). I can find properties of the system that need to be conserved. In the \(CH_4\) example we could take a look at the vibrational Hamiltonian. Solving the full problem gives us a number of normal modes. Every normal mode corresponds to a irreducible representation of the Hamiltonian. The type of irrep for every vibration is now conserved. This means that no matter what happens inside of the molecule, vibrational energy in a antisymmetric vibration will never be able to transform into a symmetric vibration. The symmetry of the vibrational energy is conserved!¹¹

This is extremely powerful and is nowadays used in spectroscopy for example as a criterion for Fermi resonance^[?]

Symmetries and gauge invariance

When building a fundamental theory such as electromagnetism, we sometimes stumble over variables we can seemingly choose arbitrarily. We can, for example, choose the electromagnetic potential to have an arbitrary o0set. (We don’t care if the plus of the battery is at 12 V and the minus at 0 V, or if the plus is at 13 V and the minus at 1 V.) The freedom to choose globally what voltage o0set any potential has is called gauge freedom or gauge invariance.

In quantum electrodynamics, one of the fundamental assumptions/findings is that the Dirac-field (the field of the electron) possesses local \(U_1\) phase symmetry. This means that we can multiply any complex phase at any position to the electron field and nothing changes.

The bare electron Lagrangian surprisingly does actually not have this symmetry. But if we impose this symmetry nontheless and adjust the Lagrangian to fit this symmetry we can derive that there needs to be an additional thing that interacts with electrons. Investigating further it can be shown that this additional thing is the electromagnetic field!

It is essentially possible to derive the existence of light from the nature of electrons and an additional symmetry requirement!

If you want to learn more about this I can highly recommend the video ’Electromagnetism as a gague theory’ by Richard Behiel.^[3]

Symmetry means ending with the beginning

There are many more applications of symmetry, and if you look around yourself and are open to perceiving the world through the lense of representation theory you will discover many more. I hope this article has given you some insights into the application, brilliance and beauty of symmetry.

So to round o0 this entire article; imagine if you will, being a shark, minding your own business. Just swimming around the ocean floor. If you want to understand how symmetry works you should definitively check out this¹² !

Bibliography